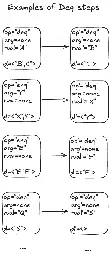
Introduction:

> Back in August, Murat Derimbas published a blog post about the paper by Herlihy and Wing that first introduced the concept of linearizability. When we move from sequential programs to concurrent ones, we need to extend our concept of what "correct" means to account for the fact that operations from different threads can overlap in time. Linearizability is the strongest consistency model for single-object systems, which means that it's the one that aligns closest to our intuitions. Other models are weaker and, hence, will permit anomalies that violate human intuition about how systems should behave. > > Beyond introducing linearizability, one of the things that Herlihy and Wing do in this paper is provide an implementation of a linearizable queue whose correctness cannot be demonstrated using an approach known as refinement mapping. At the time the paper was published, it was believed that it was always possible to use refinement mapping to prove that one specification implemented another, and this paper motivated Leslie Lamport and Martín Abadi to propose the concept of prophecy variables. > > I have long been fascinated by the concept of prophecy variables, but when I learned about them, I still couldn't figure out how to use them to prove that the queue implementation in the Herlihy and Wing paper is linearizable. (I even asked Leslie Lamport about it at the 2021 TLA+ conference). > > Recently, Lamport published a book called The Science of Concurrent Programs that describes in detail how to use prophecy variables to do the refinement mapping for the queue in the Herlihy and Wing paper. Because the best way to learn something is to explain it, I wanted to write a blog post about this. > > In this post, I'm going to assume that readers have no prior knowledge about TLA+ or linearizability. What I want to do here is provide the reader with some intuition about the important concepts, enough to interest people to read further. There's a lot of conceptual ground to cover: to understand prophecy variables and why they're needed for the queue implementation in the Herlihy and Wing paper requires an understanding of refinement mapping. Understanding refinement mapping requires understanding the state-machine model that TLA+ uses for modeling programs and systems. We'll also need to cover what linearizability actually is. > > We'll going to start all of the way at the beginning: describing what it is that a program should do.

Associated class (Brown University cs1951x)

This is a 209-page book on logical verification in Lean (4.0, the "new" version), available as a PDF.

List of Rust static and dynamic analysis tools organized by type, with:

• Name
• Description
• IR they analyze (HIR, MIR, LLVM IR, etc.)
• Bug Types
• Technology
• Maintenance (1-5 stars, whether they're frequently updated or dead)

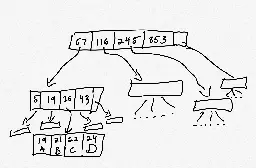
Abstract:

> I've been reading Alex Petrov's Database Internals to learn more about how databases are implemented. One of the topics covered in the book is a data structure known as the B-tree. Relational databases like Postgres, MySQL, and sqlite use B-trees as the data structure for storing the data on disk. > > I was reading along with the book as Petrov explained how B-trees work, and nodding my head. But there's a difference between feeling like you understand something (what the philosopher C. Thi Nguyen calls clarity) and actually understanding it. So I decided to model B-trees using TLA+ as an exercise in understanding it better. > > TLA+ is traditionally used for modeling concurrent systems: Leslie Lamport originally developed it to help him reason about the correctness of concurrent algorithms. However, TLA+ works just fine for sequential algorithms as well, and I'm going to use it here to model sequential operations on B-trees.

Nondeterminism is used very often in formal specifications, and not just when multi-threading or explicit randomness are involved. This article provides examples, insight into why that is, and more.

> Recently Boats wrote a blog post about Rust, mutable aliasing, and the sad story of local reasoning over many decades of computer science. I recommend that post and agree with its main points! Go read it! But I also thought I'd add a little more detail to an area it's less acutely focused on: formal methods / formal verification. > > TL;DR: support for local reasoning is a big factor in the ability to do automated reasoning about programs. Formal verification involves such reasoning. Rust supports it better than many other imperative systems languages -- even some impure functional ones! -- and formal verification people are excited and building tools presently. This is not purely by accident, and is worth understanding as part of what makes Rust valuable beyond "it doesn't need a GC". > > The rest of this post is just unpacking and giving details of one or more of the above assertions, which I'll try to address in order of plausible interestingness to the present, but I will also throw in some history because I kinda can't help myself.

The author is Graydon Hoare, the "founder" of Rust and technical lead until around 2013.

From README:

> At the heart of coq-of-rust is the translation of Rust programs to the proof system Coq 🐓. Once some Rust code is translated to Coq, it can then be verified using standard proof techniques. > > Here is an example of a Rust function: > > rust > fn add_one(x: u32) -> u32 { > x + 1 > } > > > Running coq-of-rust, it translates in Coq to: > > coq > Definition add_one (τ : list Ty.t) (α : list Value.t) : M := > match τ, α with > | [], [ x ] => > ltac:(M.monadic > (let x := M.alloc (| x |) in > BinOp.Panic.add (| M.read (| x |), Value.Integer Integer.U32 1 |))) > | _, _ => M.impossible > end. > > > Functions such as BinOp.Panic.add are part of the standard library for Rust in Coq that we provide. We can then express and verify specifications on the code in Coq.

Blog:

• Improvements in the Rust translation to Coq, part 1, part 2, part 3
• Monadic notation for the Rust translation
• Translation of Rust's core and alloc crates

The same group also recently started coq-of-python, which is the same thing but for Python:

• Translation of Python code to Coq
• Simulation of Python code in Coq

Alternate Rust-to-_ translators:

• Hax: Translate Rust to Coq (like above) or F*.
• Aeneas + Charon: Translate Rust's MIR to pure lambda calculus / F* / Coq / HOL / Lean. Currently has some strict limitations like no nested loops or closures. Paper: Aeneas: Rust verification by functional translation.

Other Rust formal verification projects:

• Creusot: Formally verifies Rust code with annotations representing preconditions/postconditions/assertions, by translating the MIR to Why3 then solving.
• Kani: Formally verifies Rust code with annotations, by using model checking powered by CBMC.
• Verus: Formally verifies a Rust DSL with syntax extensions to represent preconditions/postconditions/assertions, by using the Z3 SMT solver.

> This blog post is about Agda Core, a project to build a a formally specified core language for (a reasonable subset of) Agda together with a reference implementation of a type checker for it. If you have been following my work, you might know that I have been working on this project on and off for the past few years, yet the current version is still very much a work in progress. Hence, in the second part of this post, I will dive into a few examples of some of the more unexpected and interesting obstacles we encountered while trying to turn Agda Core from a dream into reality.

Context: Dafny is a programming language with a built-in SMT solver that can encode formally-checked statements (e.g. preconditions, postconditions, assertions).

Dafny has features of most programming languages; for example, covariant/contravariant/"non-variant" (invariant) type parameters. But in order to keep said verification sound and decidable in reasonable time, these features have extra restrictions and other complexities.

This article explains that there are 2 more "variance modes", because the of "covariant" and "invariant" variances may be "cardinality-preserving" or "not cardinality-preserving".

dafny // Most "traditional" languages have 3 variances type Foo< +CovariantParameter, NonVariantParameter, -ContravariantParameter> // Dafny has 5 type Bar< +CovariantCardinalityPreservingParameter, NonVariantCardinalityPreservingParameter, -ContravariantParameter, *CovariantNonCardinalityPreservingParameter, !NonVariantNonCardinalityPreservingParameter>

Another, very similar verified superset of Rust is Creusot. I'm not sure what the benefits/downsides of each are besides syntax tbh.

This is also similar to Kani which also verifies Rust code. However, Kani is a model checker like TLC (the model checker for TLA+), while Verus and Creusot are SMT solvers like Dafny.

Interestingly, Verus (unlike both Kani and Creusot) has its language server, which is a fork of rust-analyzer (verus-analyzer).

> Narya is eventually intended to be a proof assistant implementing Multi-Modal, Multi-Directional, Higher/Parametric/Displayed Observational Type Theory, but a formal type theory combining all those adjectives has not yet been specified. At the moment, Narya implements a normalization-by-evaluation algorithm and typechecker for an observational-style theory with Id/Bridge types satisfying parametricity, of variable arity and internality. There is a parser with user-definable mixfix notations, and user-definable record types, inductive datatypes and type families, and coinductive codatatypes, with functions definable by matching and comatching case trees.

cross-posted from: https://infosec.pub/post/9524990

> Verifiable Random Functions

It uses PRISM, a "probabilistic model checker", so not your typical theorem prover or SAT solver.

> In the past few years, we witnessed the development of multiple smart contract languages - Solidity, Viper, Michelson, Scilla etc. These languages need to enable developers to write correct, predictable behavior smart contract code. Each language development effort therefore ends up spending resources into building formal verification toolsets, compilers, debuggers and other developer tools. > In this episode, we are joined by Grigore Rosu, Professor of computer science at UIUC [University of Illinois at Urbana-Champaign] for a deep dive into the K framework. The K framework is mathematic logic and language that enables language developers to formally define all programming languages; such as C, Solidity and JavaScript. Once a language is formally specified in the K framework, the framework automatically outputs a range of formal verification toolsets, compilers, debuggers and other developer tools for it. Updates to the language can be made directly in K. This technology has massive implications for smart contract programming language development, and formal verification efforts in the blockchain space. > We also cover his efforts to express the Ethereum virtual machine using the K framework, and to develop a new virtual machine technology, called IELE, specifically tailored to the blockchain space. Check out the episode to understand a game changing technology in the formal verification and smart contract safety space. > > Topics discussed in this episode: > - Grigore's background with NASA and work on formally verified correct software > - Motivations to develop K framework > - Basic principles behind the operation of K framework > - How K deals with undefined behavior / ambiguities in a language definition > - The intersection of K framework and smart contract technology > - Runtime Verification's collaboration with Cardano > - KEVM and IELE, smart contract virtual machines developed by Runtime Verification > - Broader implications of the K framework for the blockchain industry

I saw this posted on r/ProgrammingLanguages. I hadn't heard of this language before, but it looks neat.

https://en.wikipedia.org/wiki/Dafny

Recordings are available here: https://www.nationalacademies.org/event/06-12-2023/ai-to-assist-mathematical-reasoning-a-workshop

>This development encodes category theory in Coq, with the primary aim being to allow representation and manipulation of categorical terms, as well realization of those terms in various target categories.

The community currently has no mods (as the person who requested it in the request community did not want to mod it).

If anyone wants to be a mod feel free to dm me or reply here